안녕하세요. 이번 과외 시간에서 다룰 내용은 삼각비입니다.
중학교 3학년 2학기 때 처음 배우는 내용입니다.
그런데, 경험상 많은 학생들이 3학년 2학기 과정을 건너뛰는 경우가 많았습니다.
그런데, 삼각비를 비롯하여 더 업그레이드되는 삼각함수는 고등학교 때 잠시 배우기도 하고,
이공 계열로 대학 진학을 할 경우 수도 없이 보게 될 녀석입니다.
삼각비. 이름만 들어도 어려워 보이기도 하는데, 어떤 녀석인지 이번 시간에 다루어보겠습니다.
'삼각비'에 '삼각'은 우리가 잘 아는 삼각형에서의 '삼각'에서 온 말입니다.
따라서, 삼각비는 우리가 아는 삼각형에서 이야기가 시작됩니다.

우리가 많이 보던 직각삼각형입니다.
각 변의 길이가 a, b, c라고 하고 오른쪽 모서리의 각을 θ(theta, 세타)라고 합시다.
여기서 삼각형 변의 길이 간의 비례 관계를 '삼각비'라고 부릅니다.
(중학교 3학년 때 삼각비를 배우는데, 저 또한 처음 배웠을 때 어려웠고 과외하는 입장에서 학생들 또한 어려워하더군요.)
삼각비에는 sin(사인)과 cos(코사인), tan(탄젠트)로 세 가지 종류가 있습니다.
위의 그림을 다시 참고하면,
sinθ = c/b
cosθ = c/a
tanθ = b/a
가 됩니다(이것은 약속이니 암기를 해야 합니다.).
암기를 쉽게 하는 법은 다양한데, 가장 유명한 것은 다음의 그림입니다.
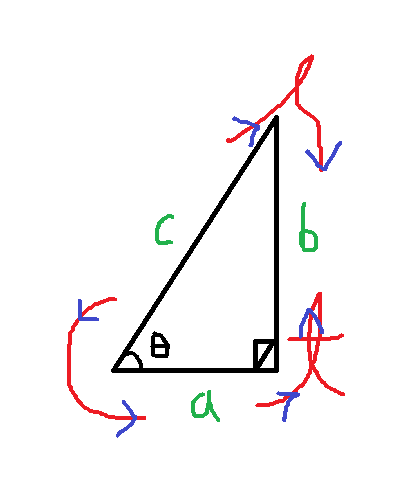
영어의 필기체를 이용하여 다음과 같이 암기하는 방법을 제시했는데, c는 cos, s는 sin, t는 tan를 나타냅니다.
문제는 직각삼각형의 방향(모습)이 정확히 위와 같아야 들어맞는다는 것입니다.
처음 배우는 학생들이 가장 어려워하는 것이 다음 그림과 같이 직각삼각형이 다른 형태로 있을 때입니다.

따라서, 새로운 암기법을 제시합니다.
1. 빗변을 찾습니다.
빗변은 직각이 마주한 변, 또는 삼각형의 세 변 중 가장 긴 변입니다.
삼각형의 세 변 중 어떤 변이 빗변인지 찾아내면 됩니다.

2. 사인, 코사인, 탄젠트의 이동방법을 암기합시다.
각 θ가 있는 점을 기준점이라고 합시다.
sin, cos, tan를 모두 사람이 걷는 방법이라고 하면,
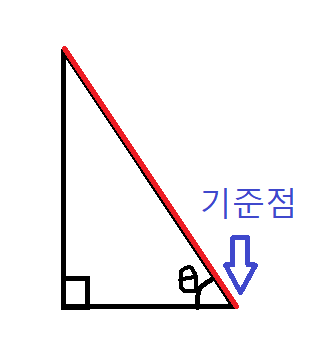
1) sin은 기준점에서 출발하여 빗변을 따라 걸어갑니다.
그때의 두 변을 순서대로 분모, 분자에 넣으면 sin이 됩니다.
2) cos은 빗변에서 기준점을 향해 들어옵니다.
그때의 두 변을 위의 방식대로 분모, 분자에 넣으면 cos이 됩니다.
3) tan는 기준점에서 빗변이 아닌 길로(직각인 각으로) 걸어갑니다.
그 때의 두변을 위의 방식대로 분모, 분자에 넣으면 tan이 됩니다.
예시로 다른 모양의 직각삼각형에 이를 적용해보고 마무리 짓겠습니다.
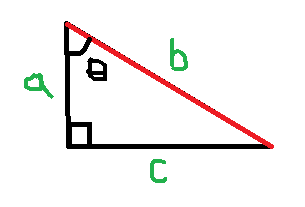
주어진 각이 있는 곳을 기준점으로 잡고, 빗변을 찾았습니다.
위의 방법에 따라 걸어가 보면 아래와 같이 됩니다.
.
.
.
sinθ = c/b , cosθ = a/b , tanθ = c/a가 됩니다.
삼각비는 삼각형 내에서만 적용이 됩니다. 즉, 0도부터 180도 내의 각에서 적용됩니다.
나중에 이 이외의 각에 대해서 삼각비를 표현하기 위해 삼각함수를 배우게 됩니다.
지금까지 삼각비를 쉽게 암기하는 법이었습니다.
공부하거나 누군가를 가르쳐주기 막막할 때 참고하세요.
댓글