[이제는, 알고싶은 수학] 1. 지수함수(기하급수적, 복리)의 이해

아직 지수함수를 배우지 않은 어린아이들도..
지금 막 지수함수에 대해 배우며, 응용 문제를 힘써 풀어내고 있는 고등학생들도..
수학을 포기한 수포자들도.. 직장인도 주부도 어르신들도...
누구나 지수함수에 대해 대략적인 느낌이 있을 것이고..적어도 필요성을 느낄 것이다.

왜냐하면, 이 세상에는 지수함수를 따라가는 것들이 굉장히 많기 때문이다.
지수함수는 박테리아가 증식할 때 박테리아의 수를 표현할 수도 있고 이처럼 분열하는 모든 것들을 표현할 수 있으며, 또 바이러스가 전파되는 속도를 나타내는 데에도 사용될 수 있다.
또 요즘처럼 제테크에 관심있는 시절 대부분의 사람들이 복리라는 말을 들어봤을텐데, 그것 역시 지수함수로써 표현된다.
이처럼 무언가가 또 무언가를 낳는 것들에 대해서는 지수함수를 모델로 사용하는 것이 마땅하다.

그럼 도대체 지수함수란 무엇인가.
함수라는 말에서부터 거부감을 느끼는 분들도 있으시겠지만..
일단은 함수에 초점을 맞추기보단, 지수의 성질과 특징에 집중해보겠다.

지수함수란..

y=2^x의 그래프

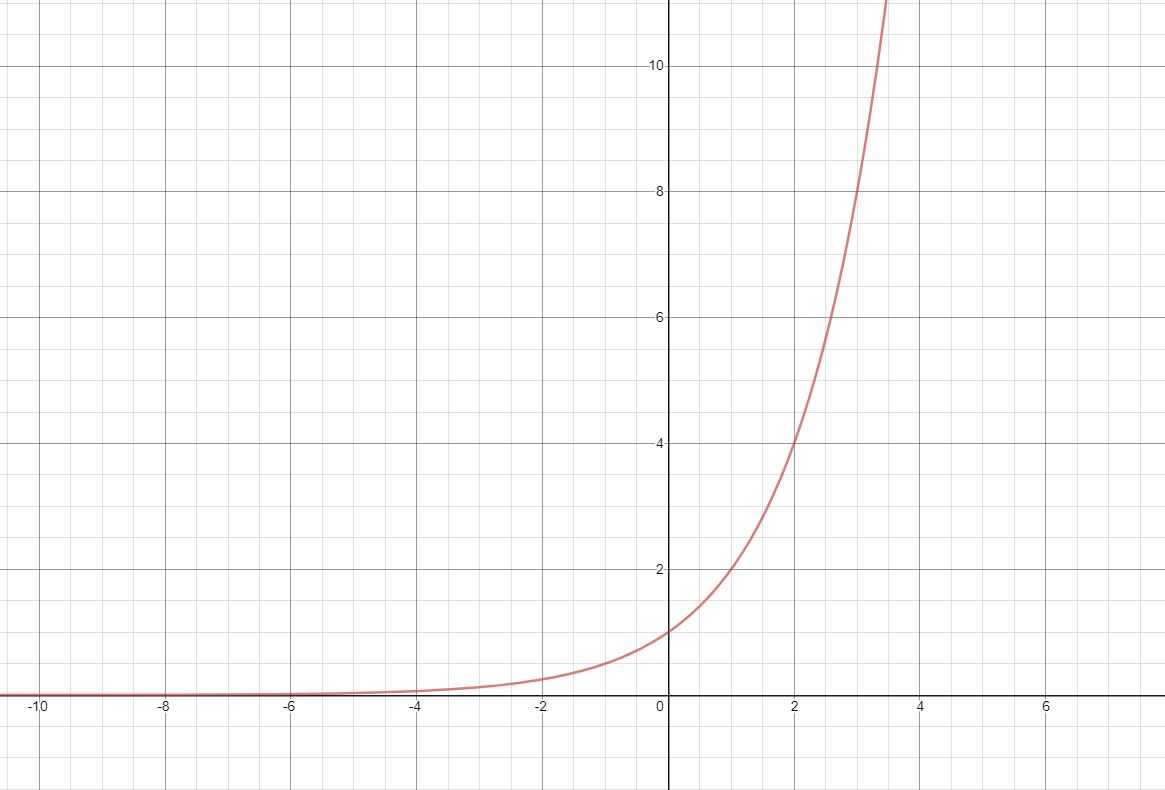
요렇게 생긴 것을 말한다. 점차 갈수록 가파르게 상승하는 곡선을 나타낸다.
지수함수의 수학적인 다양한 성질에 대해서는 나중에 다뤄보도록 하고..
여러 그림들을 보면서 숫자적인 느낌에 대해서만 알아보겠다.
저 그림을 훨씬 더 멀리서 본다면..

y=2^x그래프를 좀 더 멀리서 보면..

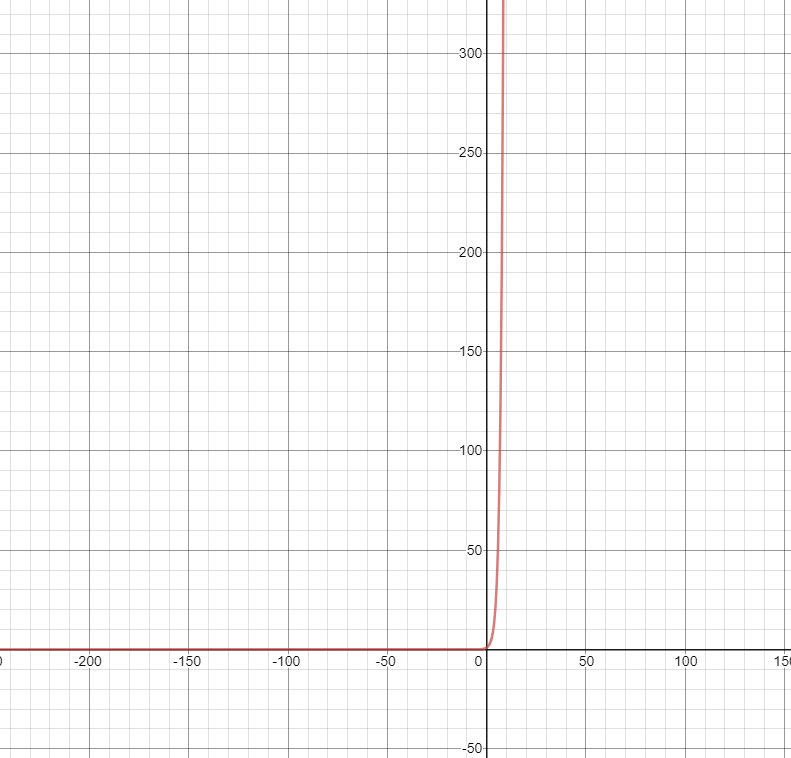
나중에는 걷잡을 수 없이 커지면서, 거의 수직 위로 뻗쳐있는 듯한 곡선을 나타낸다.
이처럼 지수함수는 다른 모든 함수에 비해 커지는 속도가 매우 빠른 무시무시한 녀석이다..
지수함수는 y=a^x의 꼴을 취하는데, 이때 지수함수의 모양을 결정짓는 것은 a이고, '밑'이라고 읽는 녀석이다. 밑은 기본적으로 0보다는 큰 양수이어야 하며(a>0)이며 1인 경우는 제외한다(a!=1).
다른 밑을 갖는 경우 위의 그림과 어떻게 달라지는지 확인해보면,

빨간색은 y=2^x의그래프, 파란색은 y=1.08^x의 그래프

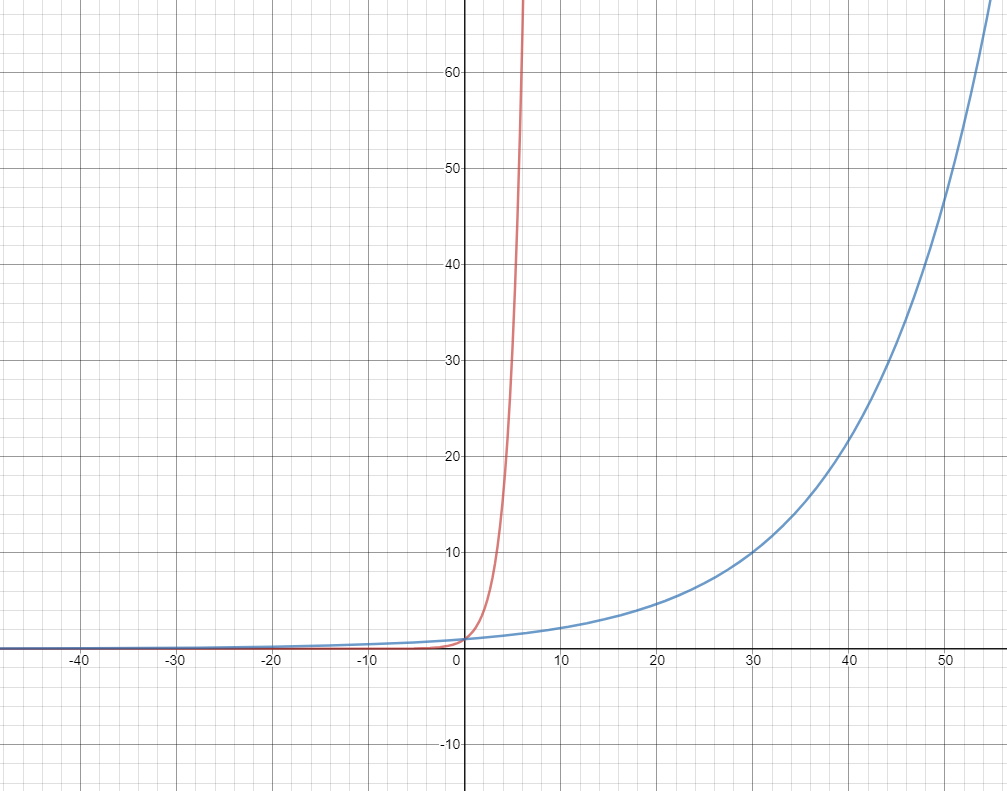
이처럼 밑을 아까와는 달리 1.08로 바꾸었을 때, 곡선이 좀 더 느리게 상승하는 것을 확인할 수 있다.
돈으로 생각하면, 당연히 8%증가율보다 100%증가율이 훨씬 빠른.. 그런 이야기다.
이번에는 밑이 1보다 작은 경우에 대해서 그려보면,

y=0.95^x의 그래프를 추가한 것.

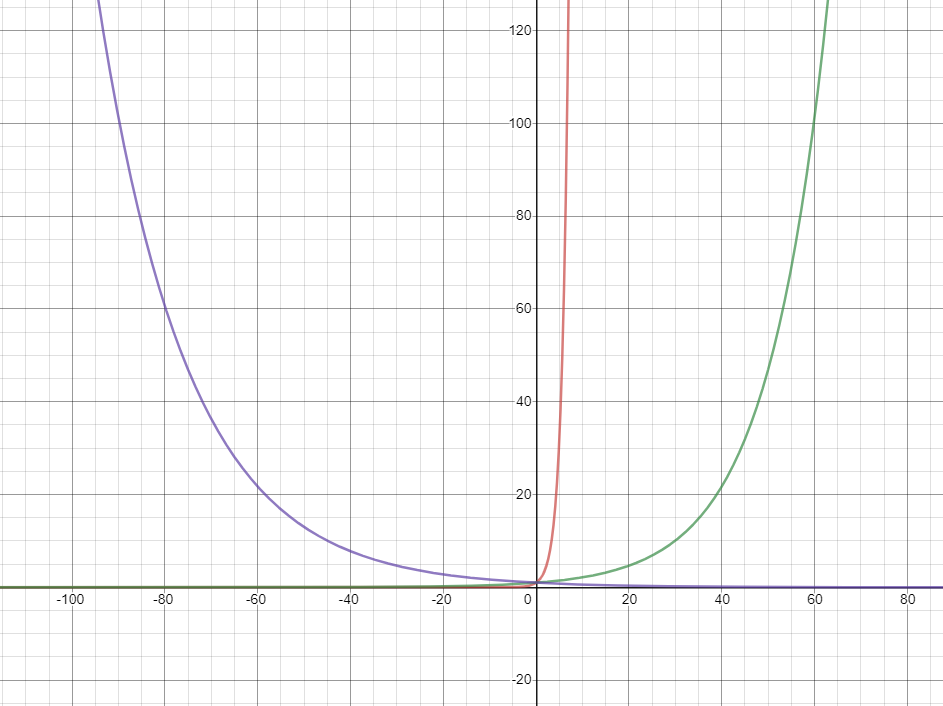
이번에는 갈수록 감소하는 그런 그래프를 띠고 있다. 세로선(y축)을 기준으로 뒤집어 놓은 듯하다.
마지막으로 다른 곡선들과의 비교를 해보면,

직선과 포물선과 지수함수

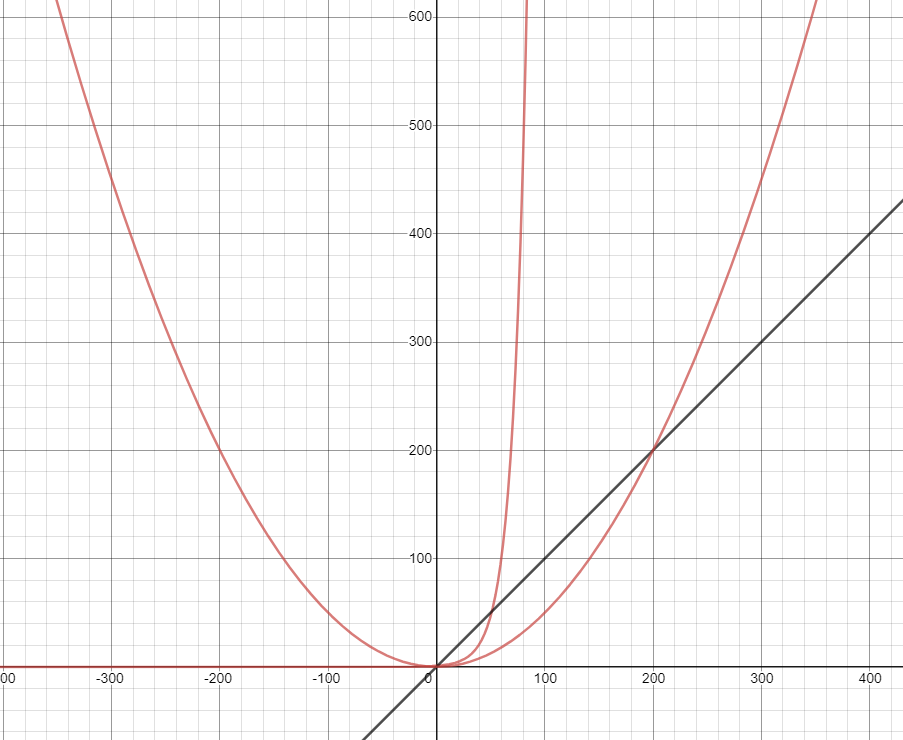
검은선인 직선과 빨간선인 포물선(이차함수) 그리고 주황색선이 지수함수이다. 눈여겨볼만한 것은 초반에는 직선이 가장 빠르다는 사실이다.
마치, '지수'는 전재산 500만원으로 연 8%씩 투자이익이 나는 상품에 투자한 사람이면, '직선'이는 500만원씩 연봉(?)을 받는 사람인 것이다. 초반에는 투자하여 벌어들인 것보다 바로 500만원씩 받는게 더 크게 느껴진다. 하지만, 조금만 지나면...그 격차는 절대 좁혀지지 않는다.
빨간선은 포물선인데 이는 y=x^2으로 지수함수와는 전혀 다른 성질을 갖게 된다. 별로 차이가 없어 보이겠지만, 이 역시 지수함수를 넘기엔 역부족이다.

이번 글에서는 지수함수의 그래프를 관찰하며, 지수함수의 느낌적인 느낌에 대해서 간단하게 알아보았다. 또한 자산과 관련된 숫자에 있어서 핵심적인 수학적인 개념이므로 모두가 잘 이해해야만 하는 녀석이다.
뒤이어서는 지수함수의 다양한 수학적인 성질이나 학문적인 응용에 대해 알아보도록 하겠다.