안녕하세요. 실생활에서 볼 수 있는 수학을 다뤄보는 시간입니다.
오늘 포스팅에서는 여러 가지 평균값, 그중에서 금융에서 알아두면 좋을 산술평균과 기하평균의 개념에 대해서 알아보도록 하겠습니다.
투자의 수익률을 따져볼 때, 관련 서적을 보다보면 산술평균 수익률과 기하평균 수익률 두 가지 개념에 대해서 소개하는 경우가 있습니다.
서적을 읽으면서도 수적인 부분은 이해하기가 쉽지 않은 만큼, 오늘 포스팅에서는 이 부분에 대해서 다루어보도록 하겠습니다.
먼저 예시를 들어보겠습니다.
중학생 철수가 5과목 국어, 수학, 영어, 사회, 과학 중간고사를 치렀습니다.
성적표를 보니,
| 과목 | 국어 | 수학 | 영어 | 사회 | 과학 | 평균 |
| 성적 | 80 | 50 | 60 | 75 | 70 | 67 |
이와 같은 성적을 받았습니다.
여기서 마지막 열에 평균은 어떻게 구한 것일까요?
과목 각각의 점수를 모두 더한 다음, 전체 과목수로 나누면 됩니다.
즉, (80+50+60+75+70) / 5 = 67로 구해집니다.
누구든지 평균을 구하라고 하면 위와 같은 방법으로 구할 것입니다.
이렇게 가장 보편적으로 사용하는 평균은 '산술평균'입니다.
산술평균은 이와 같이 모든 데이터 값의 합을 데이터 개수로 나눈 값을 의미합니다.
다음 예시입니다.

위의 그림은 가로의 길이가 9, 세로의 길이가 4인 직사각형입니다.
위 직사각형의 넓이는 얼마일까요?
4 X 9 = 36입니다.
그렇다면 이 직사각형과 넓이가 같은 정사각형의 한 변의 길이는 얼마일까요?
6 X 6 = 36이므로 한 변의 길이는 6이어야 합니다.
위의 내용을 그림으로 다시 나타내면,
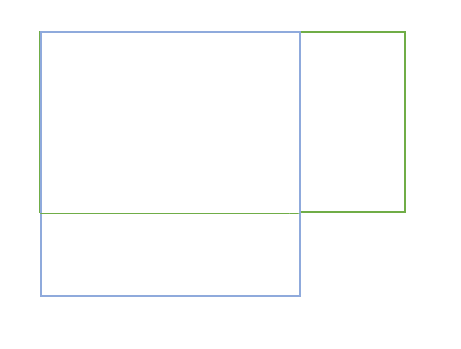
파란색 사각형은 길이가 6인 정사각형이고 초록색 사각형은 가로의 길이가 9, 세로의 길이가 4인 직사각형입니다. 위의 두 사각형은 모두 넓이가 36으로 같습니다.
이때, 정사각형의 한 변의 길이인 6이 직사각형의 가로와 세로의 길이인 4와 9의 기하평균입니다.
이를 더 간단하게 표현하면 4와 9를 곱한 값의 제곱근이 기하 평균값이 된다고 할 수 있습니다.
3차원으로 확장하여 직육면체와, 이와 부피가 같은 정육면체가 있다고 하면 직육면체의 가로, 세로, 높이 길이의 기하평균은 정육면체의 한 변의 길이와 같습니다.
예를 들어, 가로가 2, 세로가 4, 높이가 8인 직육면체라면(부피가 64인 직육면체), 그와 부피가 같은 정육면체의 한 변의 길이는 4가 되어야 합니다.
이 역시 기하 평균값은 가로, 세로, 높이를 모두 곱한 값의 세제곱근이 됩니다.
이를 n차원으로 일반화하여 나타낼 수도 있습니다만, 일단 개념적으로는 위와 같이 이해하면 됩니다.
지금까지 산술평균과 기하평균에 대해서 간단하게 다루어보았습니다.
다음 포스팅에서는 평균 수익률의 종류와 개념에 대해서 다뤄보도록 하겠습니다.
읽어주셔서 감사합니다.^^
'실생활 속 수학 > 금융' 카테고리의 다른 글
| [실생활 속 수학] 비트코인 수수료, 손익분기점, 손익 계산하기(바이비트 거래소) (1) | 2021.01.30 |
|---|---|
| [실생활 속 수학] 물타기를 하면 위험한 이유 (분할매수와 평균단가)(2) (2) | 2021.01.19 |
| [실생활 속 수학] 내분점과 외분점(분할 매수와 평균단가)(1) (1) | 2021.01.11 |
| [실생활 속 수학] 액셀로 로그차트 만들기 (2) | 2020.12.27 |
| [실생활 속 수학] 로그함수의 응용(2)(로그차트의 기울기, 상승률과 하락률) (2) | 2020.12.23 |




댓글