8월말, 혼란스러운 2020년에도 여느 때와 다름없이 고3들은 입시 준비가 한창이다.
수험생은 원하는 대학에 진학하고자 수시전형과 정시전형 중에서 자신에게 유리한 것을 준비하는데..
오늘은 전형에 상관없이 모두가 입시를 준비하면서 중요하게 여길 숫자에 대해 설명하고자 한다.
아마도 수시전형을 준비하는 학생들은 Z점수, 수능을 보는 학생들은 표준점수를 중요시 여길 것이다.
이것들은 무엇일까 알아보자.
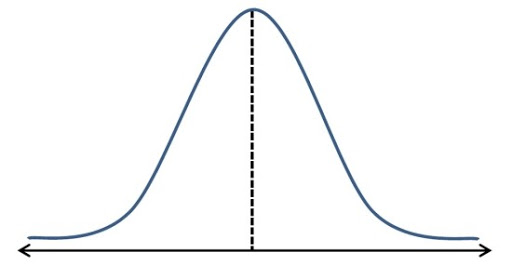
위의 그림 같이 생긴 것이 정규분포라는 놈이다.
가로축은 변량(예를 들면 점수)이고, 세로축은 확률을 나타낸다.
가운데 점선이 있는 곳이 전체 평균을 나타내는 곳이며, 평균일 확률이 가장 크고 평균에서 멀리 떨어질수록 점점 확률이 낮아지는 것을 볼 수 있다.
물론, 정규분포는 평균에 대해서 양옆으로 대칭이다.
정규분포는 어떤 자료의 통계를 낼 때 자주 사용하기에 알아두는 것이 좋다.
아마 고3 수험생들은 '확률과 통계' 단원에서 다들 한번쯤은 본 녀석일 것이다.
그럼 바로 본론으로 넘어가서 Z점수는 어떻게 구할까??

요렇게 구하는데, 수식은 나중에 살펴보고 일단 Z점수는 '(원점수-평균)/표준편차' 로 구한다. 특히, 내신시험 성적표를 받아보면 항상 원점수, 시험평균, 표준편차가 적혀있기에, 학교에 요청할 필요없이 직접 계산기로 계산 가능하다!!
예를 들어 내가 76점을 맞았는데 시험평균이 56점, 표준편차가 20이 나왔다면,
Z점수는 (76-56)/20=1.00이 나오는 것이다.
(Z점수가 1.76점 이상이 되어야 진정한 1등급이라는 말이 있는데, 이에 대해서는 다음 글에서 설명하도록 하겠다.)
그럼 표준점수는 무엇이냐?
표준점수는 Z점수와 사실상 같은 것이며, 단지 보기 좋게 숫자를 바꾸어 표기한 것이다.
국어나 수학영역처럼 만점이 100점인 시험같은 경우 '20*(Z점수)+100' 으로 구하고, 탐구영역처럼 만점이 50점인 시험은 '10*(Z점수)+50' 으로 구한다.
여기서 국어, 수학영역은 표준점수의 평균은 100점, 표준편차는 20인 것이며, 탐구영역의 표준점수 평균은 50점, 표준편차는 10이다.
대학에서도 결국 학생들의 내신점수나 수능점수를 평가할 때 표준점수나 Z점수를 활용하는데,
이렇듯 Z값을 주요 평가 수단으로 사용하기에 입시를 치르는 동안에는 Z값에 대해서 알아두는 것이 좋겠다.
충분히 직접 계산할 수 있으니, 심심하면 아마도 구겨져있을 자신의 성적표(으악!)를 꺼내 계산해보기를 바란다.
다음 시간에는 Z점수가 의미하는 바와 각 등급에 해당하는 Z점수를 환산하는 방법에 대해 다루겠다.
혼란스러운 2020년에 입시를 치르는 전국 고3들 화이팅!
'실생활 속 수학 > 입시' 카테고리의 다른 글
| 대학입학 성공한 선배의 수능 관련 썰 (0) | 2020.11.20 |
|---|---|
| Z점수(표준점수)가 갖고 있는 의미(고등 내신, 수능) (0) | 2020.10.23 |
| 입시생이라면 반드시 알아야 하는 Z점수의 모든 것(3) (고등수학-확률과 통계) (0) | 2020.10.09 |
| 입시생이라면 반드시 알아야 하는 Z점수의 모든 것(2) (고등수학-확률과 통계) (1) | 2020.09.06 |
| 대학 입시 준비 중이라면 꼭 알아야 할 표준점수의 모든 것(1) (고등수학 - 확률과 통계) (0) | 2020.09.04 |




댓글